The phasor diagram for the system in Figure 2.16 is shown in Figure 2.17, assuming that the load has a lagging power factor angle ϕ. The line or cable is represented by its impedance  , and
, and  is again neglected (being usually much smaller than
is again neglected (being usually much smaller than  . The voltage drop across the transmission line is j
. The voltage drop across the transmission line is j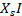 , which leads the phasor I by
, which leads the phasor I by 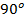 . The angle between
. The angle between  and
and  is the load angle, δ and
is the load angle, δ and
Also
From this we get the power flow equation
and the reactive power equation for the receiving end
Evidently

Fig. 2.17 Phasor diagram for Figure 2.16.
from which it can be shown that Note the symmetry between this expression and the one for
Example 1
Suppose ![clip_image002[14] clip_image002[14]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgGp_CyYXlvFJ4ahUXwiix5DGdZQOpL43BkvKW82Jbz_13HdAkKqhKQiu5fiEX1yCeFTLUuf85eoGqKBivP4FK5VbwwAM2wgXE3bdzRqogR0AlvQlofnD82VQqo3hY2BlUP6P08svTNCyA/?imgmax=800) p.u. and
p.u. and ![clip_image004[10] clip_image004[10]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj4XSkwq1Pzw7WUCumn1AJLAOgnQPbaXbkSgnP_9op1C8FzDs7qER-8beUvsIdc60heXzcwQvlFQHwzgd8TcTONAlNOjPdLAfYprhd704NYZzIM3531Uv3HjipAbobTCaMG8SJpETK_-tA/?imgmax=800) p.u.(The per‐unit system is explained in Section 2.13. If you aren’t familiar with it, try to read these examples as practice in the use of normalized (per‐unit) values. In effect, they make it possible to forget about the units of volts, amps, etc.) The transmission system has
p.u.(The per‐unit system is explained in Section 2.13. If you aren’t familiar with it, try to read these examples as practice in the use of normalized (per‐unit) values. In effect, they make it possible to forget about the units of volts, amps, etc.) The transmission system has ![clip_image006[8] clip_image006[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhp4mQUUXF7C7xC-9rgzfzZI35rDauQfDc7Fut4EA0CDNr5GjkFqo9gUd3JwxFjksogIBdP0LdQ1sACcTgUeNGSRLoQpFKD-X1OyCLELUJgXy0wIm92tuThoylXUE0vlra8IpBuzJvz6wA/?imgmax=800) . and
. and ![clip_image008[6] clip_image008[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEikAouZo0ve3su9cpwUrmK4yQ3qN7OCb9pOqZb8MRsUfyQ75g28Agri2QzJm5wg0Ky5BHSXJ6n4BxfwgK8scpb2kQpMljZvMtfoF0twzYgl9yzFTZWGilworTBnjI-fJqly-LEOoS_CsZw/?imgmax=800) is negligible. We have
is negligible. We have ![clip_image010[4] clip_image010[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg4volbTru7VjXv6QhZh2T8G9qTx9H-xfrXcX4KhcAj_w_iqaQMZrefsqDfD_m2gvjPrQSZuyCWVQYIWlO-o9BJeu29QSLX3jLWguWLSI2ip82UDngPY1V4ag_ir95b8xYrMzeEIVooVhQ/?imgmax=800) so
so ![clip_image012[4] clip_image012[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhDy14pie1VnItRMSi7urNuFCEVMr4SsLBu_R9odgb0aZcLz7EtW2FNx8kKlRD79TcxgMEKzeEUIwaFF7hDVBMIzQuFTZskMRp1pDkqVOUVoCE12M7IJzHM9Gi-SI1MuEma74NGPGASPZA/?imgmax=800) and
and ![clip_image014[4] clip_image014[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgNRPAjO5RR5YoD0PY6UC7sS08PcTxSdM1CR-9fQfylBzJzp9rBZbUqbAUR1aI5bVLoOYhpOJUWwrzXjrAyxCOQUgMddhZ_R-VjT7X3GjUvc9m-I1xzRj1b0Nia6dDYODvNF3DDJs_elJc/?imgmax=800) . Then
. Then  p.u. and
p.u. and ![clip_image018[1] clip_image018[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjnoHaROcYY53XQ41Fm62YmN4jHOxHbkyxZuG775UNavQ4-yqbz9qTk0sldQEg1FDI7LxLyEcqJv0qZ3jMsVtfC0i147ItLs4ID9WQcelJL3LT7Ee0047PEHVWlsjZhADiniw9ecg_kmTk/?imgmax=800) p.u. Thus the receiving end is generating reactive power and so is the sending end. The power factor is lagging at the sending end and leading at the receiving end. The phasor diagram is shown in Figure 2.
p.u. Thus the receiving end is generating reactive power and so is the sending end. The power factor is lagging at the sending end and leading at the receiving end. The phasor diagram is shown in Figure 2. ![clip_image020[1] clip_image020[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhNdTy_w06zYzGVk-dvjN3C3QU-02iMIvk05yunSJlMbFQkLjoCZW9Nf6dZTXCv2YAbapcqyt9OnOasvwQQT8Lp0p1gqxgPlhUJiw2scwqMAfCGSK27zJxQSyfwENwM1YbFE3TJf5o0lSU/?imgmax=800) (not to scale).
(not to scale).
Example 2 Suppose ![clip_image002[1] clip_image002[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjEKV5_xNifh9zbNcEs7xh-0XNRcEjGSsMvNLBnTBz7C0fgH2P1E7V7AEZ3ogujJHi6UUyCcmCClCIq-6vT167kKVilHdDcEqgTR0lavkDiJlYcJMHRigxWZ5pZnHYUhIVEufFvaA10mwY/?imgmax=800) p.u. while the receiving‐end voltage is reduced to
p.u. while the receiving‐end voltage is reduced to ![clip_image004[1] clip_image004[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEigufuyKU7FelmTW2Qel_nJ8kI-tToovuun3Ns0cCXZ_LXiFceokM2THV6OTQfk7A_dDl2-yBG6RQVlAWg_p_ILywr89_mz7RDYR3HaCEjWrDWGIyqx2picDoBC12agcyk-x8BnoN422n8/?imgmax=800) p.u., with
p.u., with ![clip_image006[1] clip_image006[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgc0X3g4enSJVbhaoGSzl-otiS26-k0KcKxXavZ16MyyVVkluXpHb0521xFaolHSjjyUeitnwGG9KutIoH7WTeJxfap0C3LBn2hanhsG4eADj7fwDu4xcs8XE8MfILFpaNJAkU2-8Gj6aE/?imgmax=800) . and
. and ![clip_image008[1] clip_image008[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh65Wh2nMRdQcD_mAoChf5Xt-nJ_A2NqvnWo51OVZE5cDlB1cRLusgTipgz8YJgCQTeWXpWdVhR1M7l22BF9coq_fTXCHya_KZ72f0Dccb0NTc1R8s3jv0atgcLdBEL6lhKg88LLpoKoEs/?imgmax=800) . Now
. Now ![clip_image010[1] clip_image010[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh-hG30UwJzcslOROU42-78bEPkeBqFqbzqFMPG_uc7YoNMVA6cYgrNIHFurOhULb6y-oqkP9iryIxLNOB-sPkFQpGsx5MiUUgHzrqKUCpqzU7Ve5Cwp0mDL9Z5hnkN-zxxapiF9-NiGUQ/?imgmax=800) and δ
and δ![clip_image012[1] clip_image012[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiiHUOqUvgOnBv8dy_2t9EHSmc9QIkGSuqkAQbKmpg9JmlOVlzDU7S2tcgZ7PtFaEuhYeGJCpKb2xK_FAnTaGgGpBHEfuS2VhiqC6sI5-r1xZtYNG0AHLb3uH-ZLuypUX3FomeDO8HJjQs/?imgmax=800) , slightly larger than in example 1 because
, slightly larger than in example 1 because ![clip_image014[1] clip_image014[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEglmv-nyNw96LHyVPVzFxFjqV8VPak4N2rKaisvJrj_E7ArsgD6jg7yTkt9YNKLyvJOJAhtYTXnl1oizPRK7Wgi5Yg2WNiSHC8TBJTgTtcV27RMwi-0et0tNhHcRz1SS8d0LQmdfhZjOsI/?imgmax=800) is reduced by 5%. Also
is reduced by 5%. Also ![clip_image016[1] clip_image016[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjfQFvNJ-Muqwa4FcgfqOEEqd6h1yTjqq_nQl2KOwm-R1aMHVsaUJ3CGTFQTuKzwWO243Oqv9Gjms3-UcKinAsJ95hOPMH7k4iDnnlss1CJClYOrGWrANStjNhjkVBqbj-dbnHxkWKLrEY/?imgmax=800)
 . and
. and 
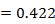 p.u. Since
p.u. Since  is positive, the sending‐end generator is generating VArs.
is positive, the sending‐end generator is generating VArs.  is also positive, meaning that the receiving‐end load is absorbing VArs. The phasor diagram is similar to that shown in Figure
is also positive, meaning that the receiving‐end load is absorbing VArs. The phasor diagram is similar to that shown in Figure  (but not to the same scale).
(but not to the same scale).
Notice that a 5% reduction in voltage at one end of the line causes a massive change in the reactive power flow. Conversely, a change in the power factor at either end tends to cause a change in the voltage. A 5% voltage swing is, of course, a very large one. Changes in the power tend to produce much smaller changes in voltage; instead, the load angle δ changes almost in proportion to the power as long as δ is fairly small ![clip_image030[1] clip_image030[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhvYN3Y5_zcd1EuqIWXQXs72J-xHjbNhJb8O4zdS5PvRETNFCnt3FoDk1tThiHqPK-Sq1THXFT80_xrhy_FQqcmYOyMq_iRDk5K1p0hyLoijGUv13SB93qIaSq8B91kVLsNcudSKrmhCPk/?imgmax=800) then
then  .
.
The transmission system has an inductive impedance and therefore we would expect it to absorb VArs. If we regard  as another impedance in series with the load impedance, we can treat it the same way. The current is obtained from
as another impedance in series with the load impedance, we can treat it the same way. The current is obtained from  p.u., and I
p.u., and I p.u. Therefore
p.u. Therefore  p.u.
p.u. 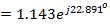 p.u. (with
p.u. (with ![clip_image014[7] clip_image014[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhAAbUoYu81xuaKGYhiDcOpXjXon6MVIO4WArchW3XhaCoM2sYNMZRuaRX62MiSRx2UyWTBKVt_z3gUv73AfpjvWakth3K92bqd2PSMcCaGBcWl4QzdO14QKUwUMRlFuN-IpTK5K8UTECo/?imgmax=800) as reference phasor). The voltage drop across
as reference phasor). The voltage drop across  is
is  and the reactive power is
and the reactive power is 
 p.u. Note that this equals the difference between
p.u. Note that this equals the difference between ![clip_image024[2] clip_image024[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgDkagciVt7MGRNF9EtMuRIBcic3PtDaizkC7Vkw3LGsn8mqTnMSVSM64R8C9JhNOfmwZwBAUZzqNH-jqM268QVnHqbFI4QP1CY-FAt9_ems7_se3jJi_GHcH1U4zFZNxhYr9P0Cxis_58/?imgmax=800) and
and ![clip_image026[2] clip_image026[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgVRnUa1mOx3kaspblFtCnKlnbuRAh7UgQpsdrtaKMsQopSyWBgVXBNKeHHkOptRpPyBuamvZJAMBWA8QuQHIosvxySl8nTpDD3KazXj_BQUekjPxR1kVkXFnc47HiuKXQZo-a6BQmg36w/?imgmax=800) .
.
We could have made a similar calculation in example 1, where  . Again this is
. Again this is  . In Example 1 also
. In Example 1 also  , which means that each end of the line is supplying half the reactive VArs absorbed in
, which means that each end of the line is supplying half the reactive VArs absorbed in ![clip_image044[1] clip_image044[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg87hoOvWh6e86jGEul39uDSi_3WFC0HkoILsgl1MIaL9FE_L5axHwJ15ojx1JaMcn9rpM_QFz2zT5M_XmudVazfUiVXLdiZbTbQ7Hnw2ewQCJYBz1UGnFagUAooZQUb7gFUq-SLJonQt8/?imgmax=800) .
.
previous Control of Power and frequency
next Three-phase systems






0 comments:
Post a Comment