Leading and lagging loads

Figure 2.7 shows a circuit with a supply system whose open-circuit voltage is E and short-circuit impedance is , where . The load impedance is

Z = 1Ω but the power factor can be unity, 0.8 lagging, or 0.8 leading. For each of these three cases, the supply voltage E can be adjusted to keep the terminal voltage V = 100 V. For each case we will determine the value of E, the power-factor angle ----, the load angle φ, the power P, the reactive power Q, and the volt-amperes S.

Unity power factor. In Figure 2.8, we have E cos δ = V = 100 and E sin δ = X_sI =0.1 × 100/1 = 10V. Therefore E = 100 +j10 = 100.5e^j5.71⁰ V. The power-factor angle is φ = cos^-1(1) = 0, δ = 5.71⁰, and S = P + jQ = VI* = 100 × 100e^j0 = 10 kVA, with P = 10kW and Q = 0.

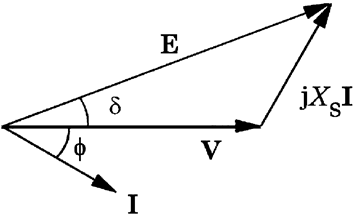
Lagging power factor. In Figure 2.9, the current is rotated negatively (i.e. clockwise) to a phase angle of ϕ = cos^-1(0.8) = -36.87°. Although I = 100 A and X_sI is still 10 V, its new orientation 'stretches' the phasor E to a larger magnitude: E = V + jX_SI = (100 +j0) + j0.1 × 100e­^-j36.87° = 106.3e^j4.32° V. When the power-factor is lagging a higher supply voltage E is needed for the same load voltage. The load angle is δ = 4.32° and S = VI* = 100 × 100e^+j36.87 = 8000 +j6000VA. Thus S = 10 kVA, P = 8 kW and Q = +6 kVAr (absorbed).

Fig. 2.7 AC supply ant load circuit.

Fig, 2,8 Phasor diagram, resistive load.

Fig, 2.9 Phasor diagrams inductive load.

Leading power factor. The leading power factor angle causes a reduction in the value of E required to keep V constant: E = 100 + j0.1 x 100e^+j36.87° = 94.3e^j4.86°V.

The load angle is δ = 4.86°, and S = 10000e^-j36.87° = 8000 - j6000; i.e. P = 8 kW and Q = 6 kVAr (generated).

We have seen that when the load power and current are kept the same, the inductive load with its lagging power factor requires a higher source voltage E, and the capacitive load with its leading power factor requires a lower source voltage. Conversely, if the source voltage E were kept constant, then the inductive load would have a lower terminal voltage V and the capacitive load would have a higher terminal voltage. As an exercise, repeat the calculations for E = 100 V and determine V in each case, assuming that Z = 1Ω with each of the three different power factors.

Fig. 2.19 Phasor diagram, capacitive boat.

We can see from this that power-factor correction capacitors (connected in parallel with an inductive load) will not only raise the power factor but will also increase the voltage. On the other hand, if the voltage is too high, it can be reduced by connecting inductors in parallel. In modern high-voltage power systems it is possible to control the voltage by varying the amount of inductive or capacitive current drawn from the system at the point where the voltage needs to be adjusted. This is called reactive compensation or static VAR control. In small, isolated power systems (such as an automotive or aircraft power system supplied from one or two generators) this is not generally necessary because the open-circuit voltage of the generator E can be varied by field control, using a voltage regulator.

previous Complex power, apparent power, real and reactive power

next Power factor correction