Complex power, apparent power, real and reactive power

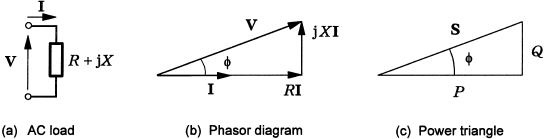
Consider a simple load R+jX with a current I and voltage V, Figure 2.6. The complex power S is deﬁned as
$S = V{I^*} = P + jQ$ (2.2)
S can be expressed graphically as the complex number P + jQ, as shown in Figure 2.6, where

P is the real power in W, kW or MW, averaged over one cycle
Q is the reactive power in VAr, kVAr, or MVAr, also averaged over one cycle
S=|S| is the apparent power or 'volt amperes', in VA, kVA or MVA

Let V be the reference phasor, and suppose that the load is inductive. Then
${\rm{I}} = I{e^{ - j\phi }} = I\cos \phi - jI\sin \phi$ (2.3)

where $\phi = {\tan ^{ - 1}}\left( {X/R} \right) = {\tan ^{ - 1}}\left( {Q/P} \right)$ . The negative phase rotation $- j\phi$ means that the current lags behind the voltage. When we take the conjugate I* and multiply by V we get

$P = VI\cos \phi {\rm{ and }}Q = VI\sin \phi$ (2.4)

Evidently P is positive and so is Q. A load that has positive reactive power is said to (absorb' VArs. Inductive loads absorb VArs. Conversely, a capacitive load would have

${\rm{I}} = I{e^{ + j\phi }} = I\cos \phi + jI\sin \phi$ (2.5)

In this case the current leads the voltage. P is still positive, but when we take the conjugate I* we get negative Q. We say that a capacitive load generates or supplies VArs.

Fig. 2.6 Development of the complex power triangle.

There is a distinction between the receiving end and the sending end. The expression $'VI\cos \phi '$ is correctly interpreted as power absorbed by the load at the receiving end. But at the sending end the generated power P is supplied to the system, not absorbed from it. The distinction is that the sending end is a source of power, while the receiving end is a sink. In Figure 2.5, for example, both ${P_S} = {E_S}I\cos {\phi _S}$ and ${P_r} = {E_r}I\cos {\phi _r}$ are positive, supplied to the system at the sending end and taken from it at the receiving end.
A similar distinction arises with reactive power. The receiving end in Figure 2.5 evidently has a lagging power factor and is absorbing VArs. The sending end has a leading power factor and is absorbing VArs. In Figure 2.9, the power factor is lagging at both the generator and the load, but the load is absorbing VArs while the generator is generating VARS. These conventions and interpretations are summarized in Table 2.4.
Note that

$\tan \phi = \frac{Q}{P}$ and $\cos \phi = \frac{P}{{\sqrt {{P^2} + {Q^2}} }}$ (2.6)

where $\cos \phi$ is the power factor.
Remember that phasors apply only when the voltage and currents are purely sinusoidal, and this expression for power factor is meaningless if either the voltage or current waveform is non-sinusoidal. A more general expression for power factor with non-sinusoidal current and waveforms is
${\rm{PF = }}\frac{{{\rm{Average Power}}}}{{{\rm{RMS volts}} \times {\rm{RMS amps}}}}$ (2.7)
previous Basic source/load relationships

next Leading and lagging loads

Electric Power Systems