Compensation and voltage control

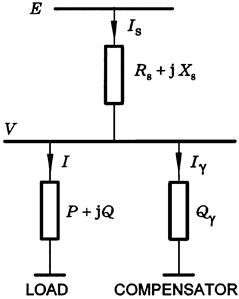
Figure 2.12 shows a one-line diagram of an AC power system, which could represent either a single-phase system, or one phase of a three-phase system. Figure 2.13 shows the phasor diagram for an inductive load.

When the load draws current from the supply, the terminal voltage V falls below the open-circuit value E. The relationship between V and the load current I is called the system load line, Figure 2.14.

The 'load' can be measured by its current I, but in power systems parlance it is the reactive volt-amperes Q of the load that is held chiefly responsible for the voltage drop. From Figures 2.12 and 2.13,

$\Delta V = E - V = {Z_S}I$ (2.10)

where I is the load current. The complex power of the load (per phase) is defined by equation (2.2), so

$I = \frac{{P - jQ}}{V}$ (2.11)

and if V = V + j0 is taken as the reference phasor we can write
$\Delta V = ({R_S} + j{X_S})\left( {\frac{{P - jQ}}{V}} \right)$ $= \frac{{{R_S}P + {X_S}Q}}{V} + j\frac{{{X_S}P - {R_S}Q}}{V} = \Delta {V_R} + j\Delta {V_X}$ (2.12)

The voltage drop ∆V has a component ∆V_R in phase with V and a component ∆V_X in quadrature with V; Figure 2.13. Both the magnitude and phase of V, relative to the open-circuit voltage E, are functions of the magnitude and phase of the load current, and of the supply impedance R_s + jX_S. Thus ∆V depends on both the real and reactive power of the load.

Fig. 2.12 Equivalent circuit of supply ant load.

Fig. 2.12 Phasor diagram (uncompensated).

Fig. 2.14 System load line.

By adding a compensating impedance or 'compensator' in parallel with the load, it is possible to maintain |V| = |E|. In Figure 2.15 this is accomplished with a purely reactive compensator. The load reactive power is replaced by the sum Q_S = Q + Q_γ, and Qγ (the compensator reactive power) is adjusted in such a way as to rotate the phasor ∆V until |V| = |E|. From equations (2.10) and (2.12),

${\left| E \right|^2} = {\left[ {V + \frac{{{R_S}P + {X_S}{Q_S}}}{V}} \right]^2} + {\left[ {\frac{{{X_S}P - {R_S}{Q_S}}}{V}} \right]^2}$ (2.13)

The value of Qγ required to achieve this 'constant voltage' condition is found by solving equation (2.13) for Q_s with V = |E|; then Q_γ = Q_s - Q. In practice the value can be determined automatically by a closed-loop control that maintains constant

Fig. 2.15 Phasor diagram, compensated for constant voltage.

voltage V. Equation (2.13) always has a solution for Q_S, implying that: A purely reactive compensator can eliminate voltage variations caused by changes in both the real and the reactive power of the load.

Provided that the reactive power of the compensator Q_γ can be controlled smoothly over a sufficiently wide range (both lagging and leading), and at an adequate rate, the compensator can perform as an ideal voltage regulator.

We have seen that a compensator can be used for power-factor correction. For example, if the power factor is corrected to unity, Q_s = 0 and Q_γ = Q. Then

$\Delta V = \left( {{R_S} + j{X_S}} \right)\frac{P}{V}$ (2.14)

which is independent of Q and therefore not under the control of the compensator. Thus: A purely reactive compensator cannot maintain both constant voltage and unity power factor at the same time.

The only exception is when P = 0, but this is not of practical interest.

System load line

In high-voltage power systems R_s is often much smaller than X_s and is ignored.

Instead of using the system impedance, it is more usual to talk about the system short- circuit level S = E²/X_S. Moreover, when voltage-drop is being considered, ∆V_x is ignored because it tends to produce only a phase change between V and E. Then

$\Delta V = \Delta {V_R}$ and $\frac{{\Delta V}}{V} = \frac{{{X_S}Q}}{{{V^2}}} \approx \frac{Q}{S}$ (2.15)

and

$V \approx E\left( {1 - \frac{Q}{S}} \right)$ (2.16)

This relationship is a straight line, as shown in Figure 2.14. It is called the system load line.

previous Power factor correction

next Control of Power and frequency

Electric Power Systems