Fault level and circuit-breaker ratings
The fault level (sometimes called short-circuit level) is a term used to describe the 'strength' of a power supply: that is, its ability to provide both current and voltage. It is defined as
Fault level = Open-circuit voltage × Short-circuit current [VA/phase]
The fault level provides a single number that can be used to select the size of circuit-breaker needed at a particular point in a power system. Circuit-breakers must interrupt fault currents (i.e. the current that flows if there is a short-circuit fault). When the contacts of the circuit-breaker are separating, there is an arc which must be extinguished (for example, by a blast of compressed air). The difficulty of extinguishing the arc depends on both the current and the system voltage. So it is convenient to take the product of these as a measure of the size or 'power' of the circuit-breaker that is needed. The fault level is used for this. The rating of a circuit-breaker should always exceed the fault level at the point where the circuit-breaker is connected –otherwise the circuit-breaker might not be capable of interrupting the fault current. This would be very dangerous: high-voltage circuit-breakers are often the final means of protection, and if they fail to isolate faults the damage can be extreme – it world like having a lightning strike that did not switch itself off.
Fig. 2.1 Thevenin equivalent circuit of one phase of a supply system (neglecting resistance).
Thevenin equivalent circuit model of a power system
At any point where a load is connected to a power system, the power system can be represented by a Thevenin equivalent circuit (The Thevenin equivalent circuit is a series equivalent circuit, in which the source is a voltage source and it is in series with the internal impedance. In the Notion equivalent circuit, the source is a current source in parallel with the internal impedance) having an open-circuit voltage E and an internal impedance Zs = Rs +jXs (see Figure 2. 1). Usually Xs is much bigger than Rs and Zs is approximately equal to jXs (as in the diagrams). The short-circuit current is Isc ≈ E/Xs and the short-circuit level is EIsc = E2/Xs in each phase. The short-circuit level is measured in volt-amperes, VA (or kVA or MVA), because E and Isc are almost in phase quadrature.
Loads and phasor diagrams
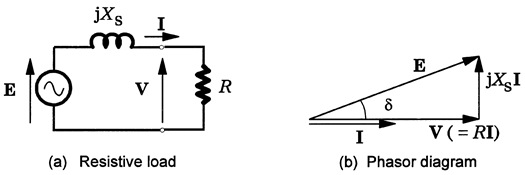
A resistive load R on an AC power system draws power and produces a phase angle shift 6 between the terminal voltage V and the open-circuit voltage E. 6 is called the load angle (see Figure 2.2). The voltage drop across the Thevenin equivalent
Fig. 2.2 Resistive load. (a) circuit diagram; and (b) phasor diagram.
Fig. 2.3 Purely inductive load. (a) circuit diagram; and (b) phasor diagram.
Fig. 2.4 Purely capacitive load. (a) circuit diagram; and (b) phasor diagram.
impedance is jXsI which is orthogonal to the terminal voltage V( = RI). Because of the orthogonality, V does not fall very much below E, even though XsI might be a sizeable fraction of E. Note that the power factor angle φ is zero for resistive loads; φ is the angle between V and I (It is assumed that the AC voltage and current are sinewaves at fundamental frequency, so+ is the phase angle at this frequency).
A purely inductive load draws no power and produces no phase-angle shift between V and E: i.e. δ = 0 (see Figure 2.3). The terminal voltage V is quite sensitive to the inductive load current because the volt-drop jXsl is directly in phase with both E and V. You might ask, 'what is the use of a load that draws no power?' One example is that shunt reactors are often used to limit the voltage on transmission and distribution systems, especially in locations remote from tap-changing transformers or generating stations. Because of the shunt capacitance of the line, the voltage tends to rise when the load is light (e.g. at night). By connecting an inductive load (shunt reactor), the voltage can be brought down to its correct value. Since the reactor is not drawing any real power (but only reactive power), there is no energy cost apart from a small amount due to losses in the windings and core.
A purely capacitive load also draws no power and produces no phase-angle shift between V and R i.e. δ = 0. The system volt-drop jXsl is directly in anti-phase with E and V, and this causes the terminal voltage V to rise above E. Again you might ask 'what is the use of a load that draws no power?' An example is that shunt capacitors are often used to raise the voltage on transmission and distribution systems, especially in locations remote from tap-changing transformers or generating stations. Because of the series inductance of the line, the voltage tends to fall when the load is heavy (e.g. mid-morning), and this is when shunt capacitors would be connected.
Fig. 2.5 Symmetrical system.
Shunt reactors and capacitors are sometimes thyristor-controlled, to provide rapid response. This is sometimes necessary near rapidly-changing loads such as electric arc furnaces or mine hoists. Of course the use of thyristors causes the current to contain harmonics, and these must usually be filtered.
The symmetrical system
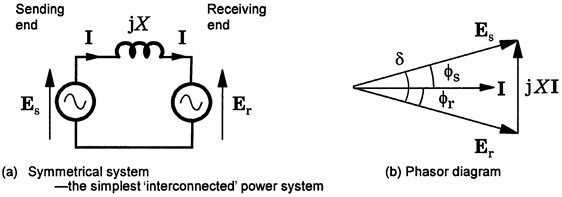
The symmetrical system is an important example – indeed the simplest example – of an interconnected power system, Figure 2.5. It comprises two synchronous machines coupled by a transmission line. It might be used, for example, as a simple model of a power system in which the main generating stations are at two locations, separated by a transmission line that is modelled by a simple inductive impedance JX. The loads (induction motors, lighting and heating systems, etc., are connected in parallel with the generators, but in the simplest model they are not even shown, because the power transmission system engineer is mostly concerned with the power flow along the line, and this is controlled by the prime-movers at the generating stations (i.e. the steam turbines, water turbines, gas turbines, wind turbines etc.).
Although the circuit diagram of a symmetrical system just looks like two generators connected by an inductive impedance, power can flow in either direction. The symmetrical system can be used to derive the power flow equation, which is one of the most important basic equations in power system operation. If Es and Er are the open-circuit voltages at the two generators, then
where δ is the phase angle between the phasors Es and Er. Note that in Figure 2.5 there are two power factor angles: φs between Es and I at the sending end, and φr between E, and I at the receiving end.
previous Power systems engineering - fundamental concepts
next Complex power, apparent power, real and reactive power
next Complex power, apparent power, real and reactive power
Posts
0 comments:
Post a Comment