Power flow and measurement

Single-phase

Suppose we have a single-phase load as in Figure 2.7 supplied with a sinusoidal voltage whose instantaneous value is . The RMS value is and the phasor value is V. If the load is linear (i.e. its impedance is constant and does not depend on the current or voltage), the current will be sinusoidal too. It leads or lags the voltage by a phase angle , depending on whether the load is capacitive or inductive. With a lagging (inductive) load, ; see Figure 2.29.

The instantaneous power is given by , so

(2.30)

This expression has a constant term and a second term that oscillates at double frequency. The constant term represents the average power : we can write this as

  (2.31)

is equal to the product of the rms voltage , the RMS current , and the power factor . The amplitude of the oscillatory term is fixed: i.e. it does not depend on the power factor. It shows that the instantaneous power varies from to and back to twice every cycle. Since the average power is VmIm/2, this represents a peak-peak fluctuation 200% of the mean power, at double frequency. The oscillation of power in single-phase circuits con- tributes to lamp flicker and causes vibration in motors and transformers, producing undesirable acoustic noise.

 

Fig. 2.29  Instantaneous current, voltage and power in a single-phase AC circuit.

Two-phase

Suppose we have a two-phase load with phases a and b, with υ_a = V_m cos ωt, i_a = I_m cos (ωt – ϕ) and υ_b = V_m sin ωt, i_b = I_m sin (ωt - ϕ). This system is said to be balanced, because the voltages and currents have the same RMS (and peak) values in both phases, and their phase angles are orthogonal. The total instantaneous power is now given by

The oscillatory term has vanished altogether, which means that the power flow is constant, with no fluctuation, and the average power P is therefore equal to the instantaneous power p. Note that if the phases become unbalanced, an oscillatory term reappears.

Three-phase
Suppose we have a three-phase load as in Figures 2.20 and 2.22, with phases a, b and c, with

This system is said to be balanced, because the voltages and currents have the same RMS (and peak) values in all three phases, and their phase angles are equi-spaced (i.e. with a 120^o symmetrical phase displacement). The total instantaneous power is now given by

As in the two-phase system, the oscillatory term has vanished. The power flow is constant, with no fluctuation, and the average power P is equal to the instantaneous power p. If the phases become unbalanced, an oscillatory term reappears.

The voltages and currents in equation (2.34) are phase quantities. In terms of line quantities, for a wye connection we have   and I_L = I_ph, whereas for a delta connection we have and V_LL = V_ph. In both cases, therefore,

where ϕ is the angle between the phasors V_ph  and I_ph.
previous Three-phase systems

next Power measurement

Three-phase systems

Most power systems (from 415 V upwards) are three‐phase systems. When the phases are balanced, the phasor diagrams and equations of one phase represent all three phases.

Why three‐phase? The main reasons for having more than one phase are as follows:

(a) better utilization of materials such as copper, iron, and insulation in lines, cables, transformers, generators and motors

(b) constant power flow

(c) diversity and security of supply and

(d) ‘natural rotation’, permitting the widespread use of AC induction motors.

Development of three‐phase systems

To achieve ‘diversity’ —that is, the ability to supply different loads from different circuits so that a failure in one circuit would not affect the others —we can use separate circuits or ‘phases’ as shown in Figure 2.18.

The power in each phase is where and are the RMS voltage and current as shown in Figure 2.18. The total power is 3. Assuming that the cable works at a certain current‐density determined by its allowable temperature rise, the total cross‐section area of conductor is 6A.

Suppose that the three phase currents are shifted in time phase by 120° from one another as shown in Figure 2.19. The RMS currents are unchanged, as is the power in each phase and the total power. The sum of the three currents is zero, and we can express this in terms of instantaneous or phasor values

and (2.23)

Fig. 2.18 Three single-phase cable.

Fig. 2.19 Three‐phase instantaneous and phasor currents.

This suggests that the circuit could be equally well served by the three‐phase connection shown in Figure 2.20, which has only half the number of conductors compared with Figure 2.18. Figure 2.20 also shows the cross‐section of a three‐phase cable capable of carrying the required current. The total cross‐section of conductor is 3, that is a saving of 50%.

In the voltage phasor diagram in Figure 20, the voltage across each phase of the load remains the same as in Figure 2.20, but the voltage between lines is increased: evidently from the geometry of the triangles

(2.24)
where V is the reference phase voltage taken as , measured between line A and the ‘star point’ of the load or the ‘neutral point’ of the supply. Likewise the phase voltage is measured between line and the star‐point of the load, and between line and the star point. The line‐line voltages are times the phase voltages. In Figure 2.20 both the load and the generator are ‘wye connected’ and in terms of the RMS values only, we have
and (2.25)

Fig. 2.20 Three‐phase connection with wye‐connected load and phasor diagram.

where is the line current and is the phase current. With wye connection they are one and the same current. The dotted line in Figure 2.20 shows the possibility of a connection between the neutral point of the supply and the star point of the load. This connection may be used to stabilize the potential of the star point where there is an excess of triplen harmonics in the current or voltage waveforms of the load.

The current and voltage in Figures 2.19 and 2.20 are displaced in phase by the power factor angle . Figure 2.21 shows a complete phasor diagram for a balanced wye‐connected load with a lagging power factor.

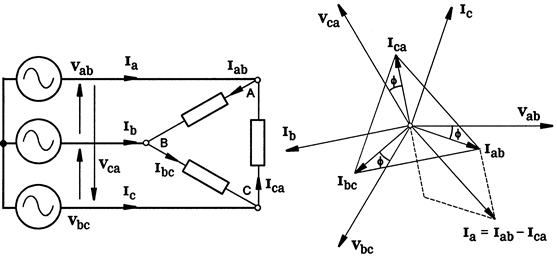
An alternative connection of the three phases is the delta connection shown in Figure 2.22 together with the construction of the phasor diagram under balanced conditions with a lagging power factor.

For the delta connection,

and (2.26)

The delta connection is used to provide a path for triplen harmonic currents. For example, when transformers operate at higher than normal voltage the magnetizing

Fig. 2.21 Phasor diagram for balanced wye‐connected load.

Fig. 2.22 Three‐phase connection with delta‐connected load and phasor diagram.

Fig. 2.23 Wye‐delta transformation.

current in each phase tends to become distorted, and the triplen harmonics are allowed to flow locally in a delta‐connected winding without entering the external circuit. In electric motors a delta winding permits the use of a larger number of turns of smaller‐gauge wire, because the phase voltage is increased while the phase current is decreased, compared with the wye connection.

 

The wye-delta transformation

A wye‐connected load can be represented by a virtual load connected in delta, and vice‐versa, Figure 2.23. To transform the delta connection into a wye connection,

; ;

where . To transform the wye connection into a delta connection,

; ; (2.28)

where

Balancing an unbalanced load

It can be shown by means of a series of diagrams, that an unbalanced linear ungrounded three‐phase load can be transformed into a balanced, real three‐phase load without changing the power exchange between source and load, by connecting an ideal reactive compensating network in parallel with it. Assume that the load is delta‐connected with admittances , as shown in Figure 2.24.

The power factor of each phase can be corrected to unity by connecting compensating admittances in parallel, as shown, where , and . The resulting network is real, Figure 2.25.

Fig. 2.24 Unbalanced delta‐connected load with power‐factor correction admittances.

Fig. 2.25 Unbalanced load corrected with unity power factor in each phase.

If we now take one of the resistive admittances, , we can connect this in a so‐called Steinmetz network with an inductor and a capacitor to produce balanced line currents as shown in Figure 2.26. The phasor diagram in Figure shows how the balanced line currents are achieved, and the resulting equivalent circuit in Figure 2.28 is real, balanced, and wye‐connected.

Fig. 2.26 Steinmetz network with balanced line currents.

Fig. 2.27 Phasor diagram for Steinmetz network.

Fig. 2.28 Balanced network resulting from compensation of with the Steinmetz network.

The resulting compensating admittances are given in equation (2.29).

        (2.29)

previous Relationships between power, reactive power, voltage levels and load angle

next Power flow and measurement