Electric Power Systems

Most power systems (from 415 V upwards) are three‐phase systems. When the phases are balanced, the phasor diagrams and equations of one phase represent all three phases.

Why three‐phase? The main reasons for having more than one phase are as follows:

(a) better utilization of materials such as copper, iron, and insulation in lines, cables, transformers, generators and motors

(b) constant power flow

(d) ‘natural rotation’, permitting the widespread use of AC induction motors.

Development of three‐phase systems

To achieve ‘diversity’ —that is, the ability to supply different loads from different circuits so that a failure in one circuit would not affect the others —we can use separate circuits or ‘phases’ as shown in Figure 2.18.

The power in each phase is

where

and

are the RMS voltage and current as shown in Figure 2.18. The total power is 3

. Assuming that the cable works at a certain current‐density determined by its allowable temperature rise, the total cross‐section area of conductor is 6A.

Suppose that the three phase currents are shifted in time phase by 120° from one another as shown in Figure 2.19. The RMS currents are unchanged, as is the power in each phase and the total power. The sum of the three currents is zero, and we can express this in terms of instantaneous or phasor values

and

(2.23)

Fig. 2.18 Three single-phase cable.

Fig. 2.19 Three‐phase instantaneous and phasor currents.

This suggests that the circuit could be equally well served by the three‐phase connection shown in Figure 2.20, which has only half the number of conductors compared with Figure 2.18. Figure 2.20 also shows the cross‐section of a three‐phase cable capable of carrying the required current. The total cross‐section of conductor is 3

, that is a saving of 50%.

In the voltage phasor diagram in Figure 20, the voltage across each phase of the load remains the same as in Figure 2.20, but the voltage between lines is increased: evidently from the geometry of the triangles

(2.24)
where V is the reference phase voltage taken as

, measured between line A and the ‘star point’ of the load or the ‘neutral point’ of the supply. Likewise the phase voltage

is measured between line

and the star‐point of the load, and

between line

and the star point. The line‐line voltages are

times the phase voltages. In Figure 2.20 both the load and the generator are ‘wye connected’ and in terms of the RMS values only, we have

and

(2.25)

Fig. 2.20 Three‐phase connection with wye‐connected load and phasor diagram.

where

is the line current and

is the phase current. With wye connection they are one and the same current. The dotted line in Figure 2.20 shows the possibility of a connection between the neutral point of the supply and the star point of the load. This connection may be used to stabilize the potential of the star point where there is an excess of triplen harmonics in the current or voltage waveforms of the load.

The current and voltage in Figures 2.19 and 2.20 are displaced in phase by the power factor angle

. Figure 2.21 shows a complete phasor diagram for a balanced wye‐connected load with a lagging power factor.

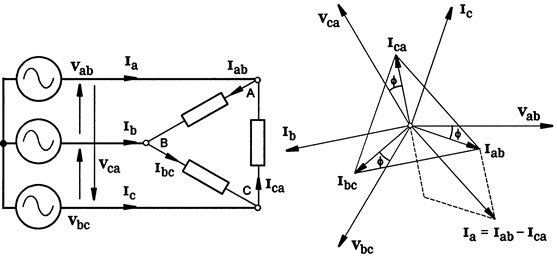
An alternative connection of the three phases is the delta connection shown in Figure 2.22 together with the construction of the phasor diagram under balanced conditions with a lagging power factor.

For the delta connection,

and

(2.26)

The delta connection is used to provide a path for triplen harmonic currents. For example, when transformers operate at higher than normal voltage the magnetizing

Fig. 2.21 Phasor diagram for balanced wye‐connected load.

Fig. 2.22 Three‐phase connection with delta‐connected load and phasor diagram.

Fig. 2.23 Wye‐delta transformation.

current in each phase tends to become distorted, and the triplen harmonics are allowed to flow locally in a delta‐connected winding without entering the external circuit. In electric motors a delta winding permits the use of a larger number of turns of smaller‐gauge wire, because the phase voltage is increased while the phase current is decreased, compared with the wye connection.

The wye-delta transformation

A wye‐connected load can be represented by a virtual load connected in delta, and vice‐versa, Figure 2.23. To transform the delta connection into a wye connection,

; ;

where . To transform the wye connection into a delta connection,

; ; (2.28)

where

Balancing an unbalanced load

It can be shown by means of a series of diagrams, that an unbalanced linear ungrounded three‐phase load can be transformed into a balanced, real three‐phase load without changing the power exchange between source and load, by connecting an ideal reactive compensating network in parallel with it. Assume that the load is delta‐connected with admittances , as shown in Figure 2.24.

The power factor of each phase can be corrected to unity by connecting compensating admittances in parallel, as shown, where , and . The resulting network is real, Figure 2.25.

Fig. 2.24 Unbalanced delta‐connected load with power‐factor correction admittances.

Fig. 2.25 Unbalanced load corrected with unity power factor in each phase.

If we now take one of the resistive admittances, , we can connect this in a so‐called Steinmetz network with an inductor and a capacitor to produce balanced line currents as shown in Figure 2.26. The phasor diagram in Figure shows how the balanced line currents are achieved, and the resulting equivalent circuit in Figure 2.28 is real, balanced, and wye‐connected.