Sub-synchronous resonance and transient stability studies are used to assess power systems' dynamic phenomena that lie somewhere in the middle, between electromagnetic transients due to switching operations and long-term dynamics associated with load frequency control. In power systems transient stability, the boiler controls and the electrical transients of the transmission network are neglected but a detailed representation is needed for the AVR and the mechanical and electrical circuits of the generator. The controls of the turbine governor are represented in some detail. In sub-synchronous resonance studies, a detailed representation of the train shaft system is mandatory (Bremner, 1996).
Arguably, transient stability studies are the most popular dynamic studies. Their main objective is to determine the synchronous generator's ability to remain stable after the occurrence of a fault or following a major change in the network such as the loss of an important generator or a large load (Stagg and El-Abiad, 1968).
Faults need to be cleared as soon as practicable. Transient stability studies provide valuable information about the critical clearance times before one or more synchronous generators in the network become unstable. The internal angles of the generator give reasonably good information about critical clearance times.
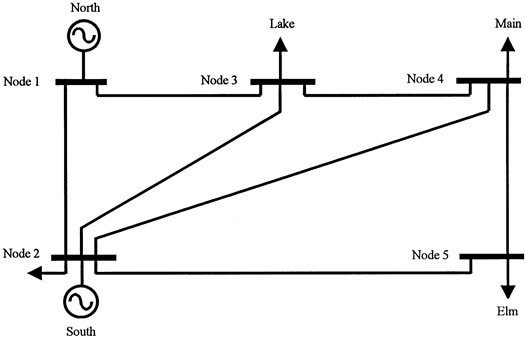
Figure 1.17 shows a five-node power system, containing two generators, seven transmission lines and four load points.
A three-phase to ground fault occurs at the terminals of Generator two, located at node two, and the transient stability study shows that both generators are stable with a fault lasting 0.1 s, whilst Generator two is unstable with a fault lasting 0.2s. Figure 1.18 shows the internal voltage angles of the two generators and their ratio of actual to rated speed. Figures 1.18(a) and (b) show the results of the fault lasting 0.1 s and (c) and (d) the results of the fault lasting 0.2 s (Stagg and EI-Abiad, 1968).
Transient stability studies are time-based studies and involve solving the differential equations of the generators and their controls, together with the algebraic equations representing the transmission power network. The differential equations are discretized using the trapezoidal rule of integration and then combined with the network's equations using nodal analysis. The solution procedure is carried out step-by-step (Arrillaga and Watson, 2001).
Fig. 1.17 A five-node power network with two generators, seven transmission lines and four loads.
Fig. 1.18 Internal voltage angles of the generators in a five-n ode system with two generators: (i) fault duration of 0.1 s: (a) internal voltage angles in degrees; (b) ratio of actual to rated speed; (ii) fault duration of 0.2s: (c) internal voltage angles in degrees; and (d) ratio of actual to rated speed (1).
Flexible alternating current transmission systems equipment responds with little delay to most power systems' disturbances occurring in their vicinity. They modify one or more key network parameters and their control objectives are: (i) to aid the system to remain stable following the occurrence of a fault by damping power oscillations; (ii) to prevent voltage collapse following a steep change in load; and (iii) to damp torsional vibration modes of turbine generator units (IEEE/CIGRE, 1995). Power system transient stability packages have been upgraded or are in the process of being upgraded to include suitable representation of FACTS controllers (Edris, 2000).
previous The dynamic response of electrical power networks
next Snapshot-like power network studies
Posts
0 comments:
Post a Comment