Compensation and voltage control

Figure 2.12 shows a one-line diagram of an AC power system, which could represent either a single-phase system, or one phase of a three-phase system. Figure 2.13 shows the phasor diagram for an inductive load.

When the load draws current from the supply, the terminal voltage V falls below the open-circuit value E. The relationship between V and the load current I is called the system load line, Figure 2.14.

The 'load' can be measured by its current I, but in power systems parlance it is the reactive volt-amperes Q of the load that is held chiefly responsible for the voltage drop. From Figures 2.12 and 2.13,

                  (2.10)

where I is the load current. The complex power of the load (per phase) is defined by equation (2.2), so

                   (2.11)

and if V = V + j0 is taken as the reference phasor we can write
          (2.12)

The voltage drop ∆V has a component ∆V_R in phase with V and a component ∆V_X in quadrature with V; Figure 2.13. Both the magnitude and phase of V, relative to the open-circuit voltage E, are functions of the magnitude and phase of the load current, and of the supply impedance R_s + jX_S. Thus ∆V depends on both the real and reactive power of the load.

Fig. 2.12 Equivalent circuit of supply ant load.

Fig. 2.12 Phasor diagram (uncompensated).

Fig. 2.14 System load line.

By adding a compensating impedance or 'compensator' in parallel with the load, it is possible to maintain |V| = |E|. In Figure 2.15 this is accomplished with a purely reactive compensator. The load reactive power is replaced by the sum Q_S = Q + Q_γ, and Qγ (the compensator reactive power) is adjusted in such a way as to rotate the phasor ∆V until |V| = |E|. From equations (2.10) and (2.12),

                     (2.13)

The value of Qγ required to achieve this 'constant voltage' condition is found by solving equation (2.13) for Q_s with V = |E|; then Q_γ = Q_s - Q. In practice the value can be determined automatically by a closed-loop control that maintains constant

Fig. 2.15 Phasor diagram, compensated for constant voltage.

voltage V. Equation (2.13) always has a solution for Q_S, implying that: A purely reactive compensator can eliminate voltage variations caused by changes in both the real and the reactive power of the load.

Provided that the reactive power of the compensator Q_γ can be controlled smoothly over a sufficiently wide range (both lagging and leading), and at an adequate rate, the compensator can perform as an ideal voltage regulator.

We have seen that a compensator can be used for power-factor correction. For example, if the power factor is corrected to unity, Q_s = 0 and Q_γ = Q. Then

                 (2.14)

which is independent of Q and therefore not under the control of the compensator. Thus: A purely reactive compensator cannot maintain both constant voltage and unity power factor at the same time.

The only exception is when P = 0, but this is not of practical interest.

System load line

In high-voltage power systems R_s is often much smaller than X_s and is ignored.

Instead of using the system impedance, it is more usual to talk about the system short- circuit level S = E²/X_S. Moreover, when voltage-drop is being considered, ∆V_x is ignored because it tends to produce only a phase change between V and E. Then

        and                     (2.15)

and

                     (2.16)

This relationship is a straight line, as shown in Figure 2.14. It is called the system load line.

previous Power factor correction

next Control of Power and frequency

Power factor correction

The load in Figure 2.7 can be expressed as an admittance Y = G + jB supplied from a voltage V, where Y = 1/Z. G is the conductance, i.e. the real part of the admittance Y, and B is the susceptance, i.e. the reactive or imaginary part of the admittance Y. The load current is I and for an inductive load the reactive component is negative (equation (2.3)) so we can write

                  (2.8)

Both V and I are phasers, and equation (2.8) is represented in the phaser diagram (Figure 2.11) in which V is the reference phaser. The voltage V and current I are in common with Figure 2.9, but Figure 2.11 shows the components of the current I and omits E and the voltage drop across the supply impedance. The load current has a 'resistive' or 'real' component I_R in phase with V, and a 'reactive' or 'imaginary' component, I_X = VB in quadrature with V. The angle between V and I is ϕ, the power-factor angle. The apparent power supplied to the load is given by equation (2 .2) with P = V²G and Q = V²B. For a capacitive load I_X is positive and Q = V²B, which is negative.

The real power P is usefully converted into heat, mechanical work, light, or other forms of energy. The reactive volt-amperes Q cannot be converted into useful forms of energy but is nevertheless an inherent requirement of the load. For example, in AC induction motors it is associated with production of flux and is often called the 'magnetizing reactive power'.

The supply current exceeds the real component by the factor 1/cos ϕ, where cos ϕ is the power factor: that is, the ratio between the real power P and the apparent power S. The power factor is that fraction of the apparent power which can be usefully converted into other forms of energy. The Joule losses in the supply cables are increased by the factor 1/ cos²ϕ. Cable ratings must be increased accordingly, and the losses must be paid for by the consumer.

The principle of power-factor correction is to compensate for the reactive power; that is, to provide it locally by connecting in parallel with the load a compensator having a purely reactive admittance of opposite sign to that of the reactive component of the load admittance. An inductive load is compensated by a capacitive admittance +jB_γ and a capacitive load by an inductive admittance -jB_γ. If the compensating admittance is equal to the reactive part of the load admittance, then for an inductive load the supply current becomes

                    (2.9)

Fig. 2.11 Phasor diagram for power factor correction.

which is in phase with V, making the overall power-factor unity. Figure 2.11 shows the phaser diagram.

With 100% compensation the supply current I_s now has the smallest value capable of supplying full power P at the voltage V, and all the reactive power required by the load is supplied locally by the compensator. The reactive power rating of the compensator is related to the rated power P of the load by Q_γ = P tan ϕ. The compensator current Q_γ/V equals the reactive current of the load at rated voltage. Relieved of the reactive requirements of the load, the supply now has excess capacity which is available for supplying other loads. The load may also be partially compensated (i.e. |Q_γ| < |Q|).

A fixed-admittance compensator cannot follow variations in the reactive power requirement of the load. In practice a compensator such as a bank of capacitors can be divided into parallel sections, each switched separately, so that discrete changes in the compensating reactive power may be made, according to the requirements of the load. More sophisticated compensators (e.g. synchronous condensers or static compensators) are capable of continuous variation of their reactive power.

The foregoing analysis has taken no account of the effect of supply voltage variations on the effectiveness of the compensator in maintaining an overall power factor of unity. In general the reactive power of a fixed-reactance compensator will not vary in sympathy with that of the load as the supply voltage varies, and a compensation 'error' will arise. Later the effects of voltage variations are examined, and we will find out what extra features the ideal compensator must have to perform satisfactorily when both the load and the supply system parameters can vary.

previous Leading and lagging loads

next Compensation and voltage control

Leading and lagging loads

Figure 2.7 shows a circuit with a supply system whose open-circuit voltage is E and short-circuit impedance is , where . The load impedance is

Z = 1Ω but the power factor can be unity, 0.8 lagging, or 0.8 leading. For each of these three cases, the supply voltage E can be adjusted to keep the terminal voltage V = 100 V. For each case we will determine the value of E, the power-factor angle ----, the load angle φ, the power P, the reactive power Q, and the volt-amperes S.

Unity power factor. In Figure 2.8, we have E cos δ = V = 100 and E sin δ = X_sI =0.1 × 100/1 = 10V. Therefore E = 100 +j10 = 100.5e^j5.71⁰ V. The power-factor angle is φ = cos^-1(1) = 0, δ = 5.71⁰, and S = P + jQ = VI* = 100 × 100e^j0 = 10 kVA, with P = 10kW and Q = 0.

Lagging power factor. In Figure 2.9, the current is rotated negatively (i.e. clockwise) to a phase angle of ϕ = cos^-1(0.8) = -36.87°. Although I = 100 A and X_sI is still 10 V, its new orientation 'stretches' the phasor E to a larger magnitude: E = V + jX_SI = (100 +j0) + j0.1 × 100e­^-j36.87° = 106.3e^j4.32° V. When the power-factor is lagging a higher supply voltage E is needed for the same load voltage. The load angle is δ = 4.32° and S = VI* = 100 × 100e^+j36.87 = 8000 +j6000VA. Thus S = 10 kVA, P = 8 kW and Q = +6 kVAr (absorbed).

Fig. 2.7 AC supply ant load circuit.

Fig, 2,8 Phasor diagram, resistive load.

Fig, 2.9 Phasor diagrams inductive load.

Leading power factor. The leading power factor angle causes a reduction in the value of E required to keep V constant: E = 100 + j0.1 x 100e^+j36.87° = 94.3e^j4.86°V.

The load angle is δ = 4.86°, and S = 10000e^-j36.87° = 8000 - j6000; i.e. P = 8 kW and Q = 6 kVAr (generated).

We have seen that when the load power and current are kept the same, the inductive load with its lagging power factor requires a higher source voltage E, and the capacitive load with its leading power factor requires a lower source voltage. Conversely, if the source voltage E were kept constant, then the inductive load would have a lower terminal voltage V and the capacitive load would have a higher terminal voltage. As an exercise, repeat the calculations for E = 100 V and determine V in each case, assuming that Z = 1Ω with each of the three different power factors.

Fig. 2.19 Phasor diagram, capacitive boat.

We can see from this that power-factor correction capacitors (connected in parallel with an inductive load) will not only raise the power factor but will also increase the voltage. On the other hand, if the voltage is too high, it can be reduced by connecting inductors in parallel. In modern high-voltage power systems it is possible to control the voltage by varying the amount of inductive or capacitive current drawn from the system at the point where the voltage needs to be adjusted. This is called reactive compensation or static VAR control. In small, isolated power systems (such as an automotive or aircraft power system supplied from one or two generators) this is not generally necessary because the open-circuit voltage of the generator E can be varied by field control, using a voltage regulator.

previous Complex power, apparent power, real and reactive power

next Power factor correction

Complex power, apparent power, real and reactive power

Consider a simple load R+jX with a current I and voltage V, Figure 2.6. The complex power S is defined as
                        (2.2)
S can be expressed graphically as the complex number P + jQ, as shown in Figure 2.6, where

P is the real power in W, kW or MW, averaged over one cycle
Q is the reactive power in VAr, kVAr, or MVAr, also averaged over one cycle
S=|S| is the apparent power or 'volt amperes', in VA, kVA or MVA

Let V be the reference phasor, and suppose that the load is inductive. Then
                      (2.3)

where . The negative phase rotation   means that the current lags behind the voltage. When we take the conjugate I* and multiply by V we get

                  (2.4)

Evidently P is positive and so is Q. A load that has positive reactive power is said to (absorb' VArs. Inductive loads absorb VArs. Conversely, a capacitive load would have

                      (2.5)

In this case the current leads the voltage. P is still positive, but when we take the conjugate I* we get negative Q. We say that a capacitive load generates or supplies VArs.

Fig. 2.6 Development of the complex power triangle.

There is a distinction between the receiving end and the sending end. The expression is correctly interpreted as power absorbed by the load at the receiving end. But at the sending end the generated power P is supplied to the system, not absorbed from it. The distinction is that the sending end is a source of power, while the receiving end is a sink. In Figure 2.5, for example, both and are positive, supplied to the system at the sending end and taken from it at the receiving end.
A similar distinction arises with reactive power. The receiving end in Figure 2.5 evidently has a lagging power factor and is absorbing VArs. The sending end has a leading power factor and is absorbing VArs. In Figure 2.9, the power factor is lagging at both the generator and the load, but the load is absorbing VArs while the generator is generating VARS. These conventions and interpretations are summarized in Table 2.4.
Note that

       and                     (2.6)

where is the power factor.
Remember that phasors apply only when the voltage and currents are purely sinusoidal, and this expression for power factor is meaningless if either the voltage or current waveform is non-sinusoidal. A more general expression for power factor with non-sinusoidal current and waveforms is
                                 (2.7)
previous Basic source/load relationships

next Leading and lagging loads

 

Basic source/load relationships

Fault level and circuit-breaker ratings

The fault level (sometimes called short-circuit level) is a term used to describe the 'strength' of a power supply: that is, its ability to provide both current and voltage. It is defined as

Fault level = Open-circuit voltage × Short-circuit current [VA/phase]

The fault level provides a single number that can be used to select the size of circuit-breaker needed at a particular point in a power system. Circuit-breakers must interrupt fault currents (i.e. the current that flows if there is a short-circuit fault). When the contacts of the circuit-breaker are separating, there is an arc which must be extinguished (for example, by a blast of compressed air). The difficulty of extinguishing the arc depends on both the current and the system voltage. So it is convenient to take the product of these as a measure of the size or 'power' of the circuit-breaker that is needed. The fault level is used for this. The rating of a circuit-breaker should always exceed the fault level at the point where the circuit-breaker is connected –otherwise the circuit-breaker might not be capable of interrupting the fault current. This would be very dangerous: high-voltage circuit-breakers are often the final means of protection, and if they fail to isolate faults the damage can be extreme – it world like having a lightning strike that did not switch itself off.

Fig. 2.1 Thevenin equivalent circuit of one phase of a supply system (neglecting resistance).

Thevenin equivalent circuit model of a power system

At any point where a load is connected to a power system, the power system can be represented by a Thevenin equivalent circuit (The Thevenin equivalent circuit is a series equivalent circuit, in which the source is a voltage source and it is in series with the internal impedance. In the Notion equivalent circuit, the source is a current source in parallel with the internal impedance) having an open-circuit voltage E and an internal impedance Z_s = R_s +jX_s (see Figure 2. 1). Usually X_s is much bigger than R_s and Z_s is approximately equal to jX_s (as in the diagrams). The short-circuit current is I_sc ≈ E/X_s and the short-circuit level is EI_sc = E²/X_s in each phase. The short-circuit level is measured in volt-amperes, VA (or kVA or MVA), because E and I_sc are almost in phase quadrature.

Loads and phasor diagrams

A resistive load R on an AC power system draws power and produces a phase angle shift 6 between the terminal voltage V and the open-circuit voltage E. 6 is called the load angle (see Figure 2.2). The voltage drop across the Thevenin equivalent

Fig. 2.2 Resistive load. (a) circuit diagram; and (b) phasor diagram.

Fig. 2.3 Purely inductive load. (a) circuit diagram; and (b) phasor diagram.

Fig. 2.4 Purely capacitive load. (a) circuit diagram; and (b) phasor diagram.

impedance is jX_sI which is orthogonal to the terminal voltage V( = RI). Because of the orthogonality, V does not fall very much below E, even though X_sI might be a sizeable fraction of E. Note that the power factor angle φ is zero for resistive loads; φ is the angle between V and I (It is assumed that the AC voltage and current are sinewaves at fundamental frequency, so+ is the phase angle at this frequency).

A purely inductive load draws no power and produces no phase-angle shift between V and E: i.e. δ = 0 (see Figure 2.3). The terminal voltage V is quite sensitive to the inductive load current because the volt-drop jX_sl is directly in phase with both E and V. You might ask, 'what is the use of a load that draws no power?' One example is that shunt reactors are often used to limit the voltage on transmission and distribution systems, especially in locations remote from tap-changing transformers or generating stations. Because of the shunt capacitance of the line, the voltage tends to rise when the load is light (e.g. at night). By connecting an inductive load (shunt reactor), the voltage can be brought down to its correct value. Since the reactor is not drawing any real power (but only reactive power), there is no energy cost apart from a small amount due to losses in the windings and core.

A purely capacitive load also draws no power and produces no phase-angle shift between V and R i.e. δ = 0. The system volt-drop jX_sl is directly in anti-phase with E and V, and this causes the terminal voltage V to rise above E. Again you might ask 'what is the use of a load that draws no power?' An example is that shunt capacitors are often used to raise the voltage on transmission and distribution systems, especially in locations remote from tap-changing transformers or generating stations. Because of the series inductance of the line, the voltage tends to fall when the load is heavy (e.g. mid-morning), and this is when shunt capacitors would be connected.

Fig. 2.5 Symmetrical system.

Shunt reactors and capacitors are sometimes thyristor-controlled, to provide rapid response. This is sometimes necessary near rapidly-changing loads such as electric arc furnaces or mine hoists. Of course the use of thyristors causes the current to contain harmonics, and these must usually be filtered.

The symmetrical system

The symmetrical system is an important example – indeed the simplest example – of an interconnected power system, Figure 2.5. It comprises two synchronous machines coupled by a transmission line. It might be used, for example, as a simple model of a power system in which the main generating stations are at two locations, separated by a transmission line that is modelled by a simple inductive impedance JX. The loads (induction motors, lighting and heating systems, etc., are connected in parallel with the generators, but in the simplest model they are not even shown, because the power transmission system engineer is mostly concerned with the power flow along the line, and this is controlled by the prime-movers at the generating stations (i.e. the steam turbines, water turbines, gas turbines, wind turbines etc.).

Although the circuit diagram of a symmetrical system just looks like two generators connected by an inductive impedance, power can flow in either direction. The symmetrical system can be used to derive the power flow equation, which is one of the most important basic equations in power system operation. If E_s and E_r are the open-circuit voltages at the two generators, then

                         (2.1)

where δ is the phase angle between the phasors E_s and E_r. Note that in Figure 2.5 there are two power factor angles: φ_s between E_s and I at the sending end, and φ_r between E, and I at the receiving end.

previous Power systems engineering - fundamental concepts
next Complex power, apparent power, real and reactive power

Power systems engineering - fundamental concepts

Reactive power control

In an ideal AC power system the voltage and frequency at every supply point would be constant and free from harmonics, and the power factor would be unity. In particular these parameters would be independent of the size and characteristics of consumers' loads. In an ideal system, each load could be designed for optimum performance at the given supply voltage, rather than for merely adequate performance over an unpredictable range of voltage. Moreover, there could be no interference between different loads as a result of variations in the current taken by each one (Miller, 1982).

In three-phase systems, the phase currents and voltages must also be balanced ( Unbalance causes negative-sequence current which produces a backward-rotating field in rotating AC machines, causing torque fluctuations and power loss with potential overheating). The stability of the system against oscillations and faults must also be assured. All these criteria add up to a notion of power quality. A single numerical definition of power quality does not exist, but it is helpful to use quantities such as the maximum fluctuation in rms supply voltage averaged over a stated period of time, or the total harmonic distortion (THD), or the 'availability' (i.e. the percentage of time, averaged over a period of, say, a year, for which the supply is uninterrupted).

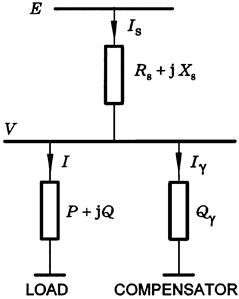
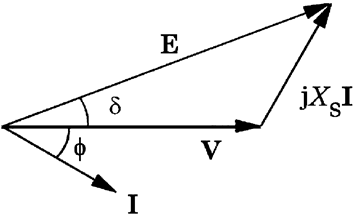
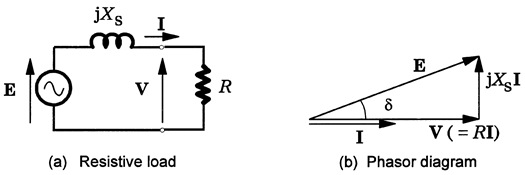
The maintenance of constant frequency requires an exact balance between the overall power supplied by generators and the overall power absorbed by loads, irrespective of the voltage. However, the voltage plays an important role in maintaining the stability of power transmission, as we shall see. Voltage levels are very sensitive to the flow of reactive power and therefore the control of reactive power is important. This is the subject of reactive compensation. Where the focus is on individual loads, we speak of load compensation, and this is the main subject of this chapter along with several related fundamental topics of power systems engineering.

Load compensation is the management of reactive power to improve the quality of supply at a particular load or group of loads. Compensating equipment — such as power-factor correction equipment—is usually installed on or near to the consumer's premises. In load compensation there are three main objectives:

• power-factor correction
• improvement of voltage regulation ('Regulation' is an old-fashioned term used to denote the variation of voltage when current is drawn from the system)
• load balancing.

Power-factor correction and load balancing are desirable even when the supply voltage is 'stiff': that is, even when there is no requirement to improve the voltage regulation. Ideally the reactive power requirements of a load should be provided locally, rather than drawing the reactive component of current from a remote power station. Most industrial loads have lagging power factors; that is, they absorb reactive power. The load current therefore tends to be larger than is required to supply the real power alone. Only the real power is ultimately useful in energy conversion and the excess load current represents a waste to the consumer, who has to pay not only for the excess cable capacity to carry it, but also for the excess Joule loss in the supply cables. When load power factors are low, generators and distribution networks cannot be used at full efficiency or full capacity, and the control of voltage throughout the network can become more difficult. Supply tariffs to industrial customers usually penalize low power-factor loads, encouraging the use of power-factor correction equipment.

In voltage regulation the supply utilities are usually bound by statute to maintain the voltage within defined limits, typically of the order of 15% at low voltage, averaged over a period of a few minutes or hours. Much more stringent constraints are imposed where large, rapidly varying loads could cause voltage dips hazardous to the operation of protective equipment, or flicker annoying to the eye.

The most obvious way to improve voltage regulation would be to 'strengthen' the power system by increasing the size and number of generating units and by making the network more densely interconnected. This approach is costly and severely constrained by environmental planning factors. It also raises the fault level and the required switchgear ratings. It is better to size the transmission and distribution system according to the maximum demand for real power and basic security of supply, and to manage the reactive power by means of compensators and other equipment which can be deployed more flexibly than generating units, without increasing the fault level.

Similar considerations apply in load balancing. Most AC power systems are three-phase, and are designed for balanced operation. Unbalanced operation gives rise to components of current in the wrong phase-sequence (i.e. negative- and zero-sequence components). Such components can have undesirable effects, including additional losses in motors and generating units, oscillating torque in AC machines, increased ripple in rectifiers, malfunction of several types of equipment, saturation of transformers, and excessive triplen harmonics and neutral currents [Triplen (literally triple-n) means harmonies of order 3n, where n is an integer].

The harmonic content in the voltage supply waveform is another important measure in the quality of supply. Harmonics above the fundamental power frequency are usually eliminated by filters. Nevertheless, harmonic problems often arise together with compensation problems and some types of compensator even generate harmonics which must be suppressed internally or filtered.

The ideal compensator would:

• supply the exact reactive power requirement of the load;
  
• present a constant-voltage characteristic at its terminals; and
  
• be capable of operating independently in the three phases.

In practice, one of the most important factors in the choice of compensating equipment is the underlying rate of change in the load current, power factor, or impedance. For example, with an induction motor running 24 hours/day driving a constant mechanical load (such as a pump), it will often suffice to have a fixed power-factor correction capacitor. On the other hand, a drive such as a mine hoist has an intermittent load which will vary according to the burden and direction of the car, but will remain constant for periods of one or two minutes during the travel. In such a case, power-factor correction capacitors could be switched in and out as required. An example of a load with extremely rapid variation is an electric arc furnace, where the reactive power requirement varies even within one cycle and, for a short time at the beginning of the melt, it is erratic and unbalanced. In this case a dynamic compensator is required, such as a TCR or a saturated-reactor compensator, to provide sufficiently rapid dynamic response.

Steady-state power-factor correction equipment should be deployed according to economic factors including the supply tariff, the size of the load, and its uncompensated power factor. For loads which cause fluctuations in the supply voltage, the degree of variation is assessed at the 'point of common coupling' (PCC), which is usually the point in the network where the customer's and the supplier's areas of responsibility meet: this might be, for example, the high-voltage side of the distribution transformer supplying a particular factory.

Loads that require compensation include arc furnaces, induction furnaces, arc welders, induction welders, steel rolling mills, mine winders, large motors (particularly those which start and stop frequently), excavators, chip mills, and several others. Non-linear loads such as rectifiers also generate harmonics and may require harmonic filters, most commonly for the 5th and 7th but sometimes for higher orders as well. Triplen harmonics are usually not filtered but eliminated by balancing the load and by trapping them in delta-connected transformer windings.

The power-factor and the voltage regulation can both be improved if some of the drives in a plant are synchronous motors instead of induction motors, because the synchronous motor can be controlled to supply (or absorb) an adjustable amount of reactive power and therefore it can be used as a compensator. Voltage dips caused by motor starts can also be avoided by using a 'soft starter', that is, a phase-controlled thyristor switch in series with the motor, which gradually ramps the motor voltage from a reduced level instead of connecting suddenly at full voltage.

Load	Limits of voltage fluctuation
Large motor starts	1-3% depending on frequency
Mine winders, excavators, large motor drives	1-3% at distribution voltage level 0.5 – 1.5% at transmission voltage level
Welding plant	1/4-2% depending on frequency
Induction furnaces	Up to 1%
Arc furnaces	<1/2%

Table 2.1 Typical voltage fluctuation standards.

Continuous and short-time reactive power requirements. Rated voltage and limits of voltage variation. Accuracy of voltage regulation required. Response time of the compensator for a specified disturbance. Maximum harmonic distortion with compensator in service. Performance with unbalanced supply voltages and/or with unbalanced load. Environmental factors: noise level; indoor/outdoor installation; temperature, humidity, pollution, wind and seismic factors; leakage from transformers, capacitors, cooling systems. Cabling requirements and layout; access, enclosure, grounding; provision for future expansion; redundancy and maintenance provisions. protection arrangements for the compensator and coordination with other protection systems, including reactive power limits if necessary. Energization procedure and precautions.

Table 2.2 Factors to consider in specifying compensating equipment.

Standards for the quality, of supply. One very noticeable effect of supply voltage variations is flicker especially in tungsten filament lamps. Slow variations of up to 3% may be tolerable, but rapid variations within the range of maximal visual sensitivity (between I and 25 Hz) must be limited to 0.25% or less. A serious consequence of undervoltage is the overcurrent that results from the fact that AC motors run at a speed which is essentially determined by the frequency, and if the voltage is low the current must increase in order to maintain the power. On the other hand, overvoltage is damaging to insulation systems.

Table 2.1 gives an idea of the appropriate standards which might be applied in different circumstances, but local statutes and conditions should be studied in each individual case.

Specification of a load compensator. Some of the factors which need to be considered when specifying a load compensator are summarized in Table 2.2.

Conventions used in power engineering

In power engineering it is helpful to have a set of conventions for symbols. Unfortunately many people disregard conventions, and this causes confusion. There is no universal standard, but the simple conventions given in Table 2.3 are widely used, practical, and consistent with most classic textbooks.

Type	What is meant	Examples
Lower-case italic	Instantaneous values	V, i
Upper-case italic	RMS values or DC values Resistance, reactance, and impedance magnitude Inductance and capacitance	V, I R, X Z L, C
Upper-case boldface roman	Phasors Impedance	V, I Z

Table 2.3 Font and symbol conventions

In handwritten work, you can't really use boldface, so use a bar or arrow or tilde — preferably over the symbol, e.g.Subscripts can be roman or italic; it is a matter of style

In three-phase systems, various conventions are used for the subscripts used to denote the three phases. In Europe (particularly Germany): U, V, W. In the UK: R, Y, B (for red, yellow, blue), or a, b, c. In the United States: a, b, c or A, B, C. You will also see I, 2, 3 used: this seems an obvious choice, but if you are working with symmetrical components these subscripts can be confused with the positive, negative, and zero-sequence subscripts I, 2, 0 (sometimes +, -, 0). The best advice is to be very careful!

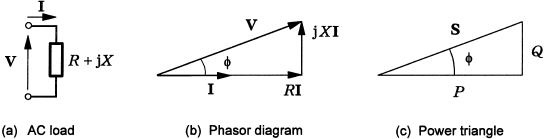
Never confuse phasor values with scalar values!

	Examples
Typeset	Comment
V=RI	RMS AC; or DC
V=jXI	V and I are phasores X is a scalar (reactance) jX is an impedance (complex)
Z=R+jX	Z is complex (impedance) R is scalar (resistance) X is scalar (reactance)
v=Vmcosωt	v is an instantaneous value Vm is a fixed scalar value

previous The role of computers in the monitoring, control and planning of power networks

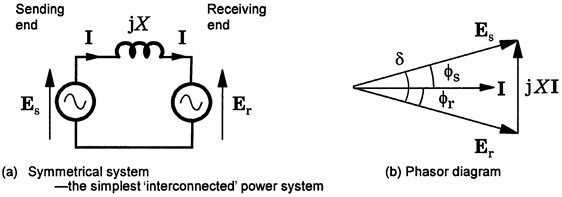
next Basic source/load relationships

Random nature of system load

The system load varies continuously with time in a random fashion. Significant changes occur from hour to hour, day to day, month to month and year to year (Gross and Galiana, 1987). Figure 1.20 shows a typical load measured in a distribution substation for a period of four days.

The random nature of system load may be included in power flow studies and this finds useful applications in planning studies and in the growing 'energy stock market'. Some possible approaches for modelling random loads within a power flow study are:

1. modelling the load as a distribution function, e.g. normal distribution;
2. future load is forecast by means of time series analysis based on historic values, then normal power flow studies are performed for each forecast point;
3. the same procedure as in two but load forecasting is achieved using Neural Networks.

Non-linear loads

Many power plant components have the ability to draw non-sinusoidal currents and, under certain conditions, they distort the sinusoidal voltage waveform in the power network. In general, if a plant component is excited with sinusoidal input and produces non-sinusoidal output, then such a component is termed non-linear, otherwise, it is termed linear (Atha and Madrigal, 2001). Among the non-linear power plant components we have: 

Fig. 1.20 A typical load measured at a distribution substation.

• power electronics equipment
• electric arc furnaces
• large concentration of energy saving lamps
• saturated transformers
• rotating machinery.

Some of the more common adverse effects caused by non-linear equipment are:

• the breakdown of sensitive industrial processes
• permanent damage to utility and consumer equipment
• additional expenditure in compensating and filtering equipment
• loss of utility revenue
• additional losses in the network
• overheating of rotating machinery
• electromagnetic compatibility problems in consumer installations
• interference in neighboring communication circuits
• spurious tripping of protective devices.

previous Power Network fault studies

next The role of computers in the monitoring, control and planning of power networks

Power Network fault studies

If it is assumed that the power network is operating in steady state and that a sudden change takes place due to a faulty condition, then the network will enter a dynamic state. Faults have a variable impact over time, with the highest values of current being present during the first few cycles after the disturbance has occurred. This can be appreciated from Figure 1.19, where a three-phase, short-circuit at the terminals of a synchronous generator give rise to currents that clearly show the transient and steady (sustained) states. The figure shows the currents in phases a, b and c, as well as the field current. The source of this oscillogram is (Kimbark, 1995).

Faults are unpredictable events that may occur anywhere in the power network. Given that faults are unforeseen events, strategies for dealing with them must be decided well in advance (Anderson, 1973). Faults can be divided into those involving a single (nodal) point in the network, i.e. shunt faults, and those involving two points in one or more phases in a given plant component, i.e. series faults. Simultaneous faults involve any combination of the above two kinds of faults in one or more locations in the network. The following are examples of shunt faults:

Fig. 1.19 Short-circuit currents of a synchronous generator (© 1995 IEEE).

1. three-phase-to-ground short-circuit
2. one-phase-to-ground short-circuit
3. two-phase short-circuit
4. two-phase-to-ground short-circuit.

The following are examples of series faults:

1. one-phase conductor open
2. two-phase conductors open
3. three-phase conductors open.

In addition to the large currents flowing from the generators to the point in fault following the occurrence of a three-phase short-circuit, the voltage drops to extremely low values for the duration of the fault. The greatest voltage drop takes place at the point in fault, i.e. zero, but neighbouring locations will also be affected to varying degrees. In general, the reduction in root mean square (rms) voltage is determined by the electrical distance to the short-circuit, the type of short-circuit and its duration.

The reduction in runs voltage is termed voltage sag or voltage dip. Incidents of this are quite widespread in power networks and are caused by short-circuit faults, large motors starting and fast circuit breaker reclosures. Voltage sags are responsible for spurious tripping of variable speed motor drives, process control systems and computers. It is reported that large production plants have been brought to a halt by sags of 100 ms duration or less, leading to losses of hundreds of thousands of pounds (McHattie, 1998). These kinds of problems provided the motivation for the development of Custom Power equipment (Hingorani, 1995).

previous Snapshot-like power network studies

next Random nature of system load

Snapshot-like power network studies

Power flow studies

Although in reality the power network is in a continuous dynamic state, it is useful to assume that at one point the transient produced by the last switching operation or topology change has died out and that the network has reached a state of equilibrium, i.e. steady state. This is the limiting case of long-term dynamics and the time frame of such steady state operation would be located at the far right-hand side of Figure 1.16. The analysis tool used to assess the steady state operation of the power system is known as Load Flow or Power Flow (Arrillaga and Watson, 2001), and in its most basic form has the following objectives:

• to determine the nodal voltage magnitudes and angles throughout the network;
• to determine the active and reactive power flows in all branches of the network;
• to determine the active and reactive power contributed by each generator;
• to determine active and reactive power losses in each component of the network.

In steady state operation, the plant components of the network are described by their impedances and loads are normally recorded in MW and MVAr. Ohm's law and Kirchhoff's laws are used to model the power network as a single entity where the nodal voltage magnitude and angle are the state variables. The power flow is a non-linear problem because, at a given node, the power injection is related to the load impedance by the square of the nodal voltage, which itself is not known at the beginning of the study. Thus, the solution has to be reached by iteration. The solution of the non-linear set of algebraic equations representing the power flow problem is achieved efficiently using the Newton-Raphson method. The generators are represented as nodal power injections because in the steady state the prime mover is assumed to drive the generator at a constant speed and the AVR is assumed to keep the nodal voltage magnitude at a specified value.

Flexible alternating current transmission systems equipment provides adaptive regulation of one or more network parameters at key locations. In general, these controllers are able to regulate either nodal voltage magnitude or active power within their design limits. The most advanced controller, i.e. the UPFC, is able to exert simultaneous control of nodal voltage magnitude, active power and reactive power. Comprehensive models of FACTS controllers suitable for efficient, large-scale power flow solutions have been developed recently (Fuerte-Esquivel, 1997).

Optimal power flow studies

An optimal power flow is an advanced form of power flow algorithm. Optimal power flow studies are also used to determine the steady state operating conditions of power networks but they incorporate an objective function which is optimized without violating system operational constraints. The choice of the objective function depends on the operating philosophy of each utility company. However, active power generation cost is a widely used objective function. Traditionally, the constraint equations include the network equations, active and reactive power consumed at the load points, limits on active and reactive power generation, stability and thermal limits on transmission lines and transformers. Optimal power flow studies provide an effective tool for reactive power management and for assessing the effectiveness of FACTS equipment from the point of view of steady state operation. Comprehensive models of FACTS controllers suitable for efficient, large-scale optimal power flow solutions have been developed recently (Ambriz-Perez, 1998).

previous Transient stability in power system
next Power Network fault studies

Transient stability in power system

Sub-synchronous resonance and transient stability studies are used to assess power systems' dynamic phenomena that lie somewhere in the middle, between electromagnetic transients due to switching operations and long-term dynamics associated with load frequency control. In power systems transient stability, the boiler controls and the electrical transients of the transmission network are neglected but a detailed representation is needed for the AVR and the mechanical and electrical circuits of the generator. The controls of the turbine governor are represented in some detail. In sub-synchronous resonance studies, a detailed representation of the train shaft system is mandatory (Bremner, 1996).

Arguably, transient stability studies are the most popular dynamic studies. Their main objective is to determine the synchronous generator's ability to remain stable after the occurrence of a fault or following a major change in the network such as the loss of an important generator or a large load (Stagg and El-Abiad, 1968).

Faults need to be cleared as soon as practicable. Transient stability studies provide valuable information about the critical clearance times before one or more synchronous generators in the network become unstable. The internal angles of the generator give reasonably good information about critical clearance times.

Figure 1.17 shows a five-node power system, containing two generators, seven transmission lines and four load points.

A three-phase to ground fault occurs at the terminals of Generator two, located at node two, and the transient stability study shows that both generators are stable with a fault lasting 0.1 s, whilst Generator two is unstable with a fault lasting 0.2s. Figure 1.18 shows the internal voltage angles of the two generators and their ratio of actual to rated speed. Figures 1.18(a) and (b) show the results of the fault lasting 0.1 s and (c) and (d) the results of the fault lasting 0.2 s (Stagg and EI-Abiad, 1968).

Transient stability studies are time-based studies and involve solving the differential equations of the generators and their controls, together with the algebraic equations representing the transmission power network. The differential equations are discretized using the trapezoidal rule of integration and then combined with the network's equations using nodal analysis. The solution procedure is carried out step-by-step (Arrillaga and Watson, 2001).

Fig. 1.17 A five-node power network with two generators, seven transmission lines and four loads.

Fig. 1.18 Internal voltage angles of the generators in a five-n ode system with two generators: (i) fault duration of 0.1 s: (a) internal voltage angles in degrees; (b) ratio of actual to rated speed; (ii) fault duration of 0.2s: (c) internal voltage angles in degrees; and (d) ratio of actual to rated speed (1).

Flexible alternating current transmission systems equipment responds with little delay to most power systems' disturbances occurring in their vicinity. They modify one or more key network parameters and their control objectives are: (i) to aid the system to remain stable following the occurrence of a fault by damping power oscillations; (ii) to prevent voltage collapse following a steep change in load; and (iii) to damp torsional vibration modes of turbine generator units (IEEE/CIGRE, 1995). Power system transient stability packages have been upgraded or are in the process of being upgraded to include suitable representation of FACTS controllers (Edris, 2000).

previous The dynamic response of electrical power networks

next Snapshot-like power network studies